Methods for Pulsed-Laser Operation
Methods for Pulsed-Laser Operation
Methods for Pulsed-Laser Operation
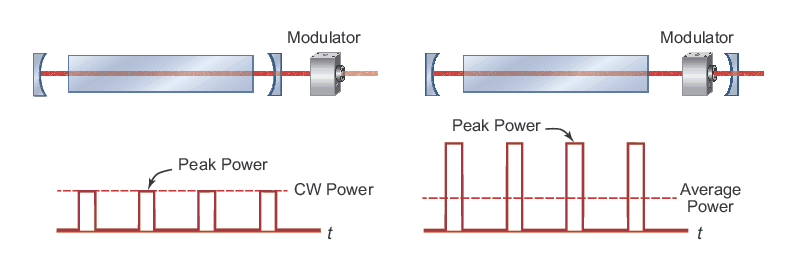
A laser operating in CW mode has constant output power as a function of time. This is the result of reaching a steady-state condition where balance is maintained between the laser cavity gain (dictated by the population inversion which is proportional to the pumping rate) and loss (which includes the cavity losses and the stimulated emission rate). As discussed in Laser Light Characteristics, it is often desirable to operate lasers in a pulsed mode since this can significantly increase the peak output power. Pulsed-laser operation can be achieved by sending a CW laser output through an external modulator that acts as a switch allowing light to transmit for only short time periods (see Figure 1, left). This simple method has many disadvantages. Since most of the light is blocked by the modulator, the method is very inefficient. Furthermore, the peak power can never exceed the average power of the CW source. The duration of the pulse is also limited by the speed of the modulator. A more efficient method uses an internal, intracavity modulation process (see Figure 1, right). By modulating the gain or loss in the cavity, the lasing process can be effectively switched on and off. Energy can be either (i) stored in the laser medium as a large population inversion that can be rapidly released to permit lasing or (ii) maintained in the resonator until it is allowed to escape. These methods permit pulsed-laser output with peak powers that significantly exceed those afforded by CW lasers. The most common methods for achieving laser pulses using internal modulation are discussed next.
Gain Switching
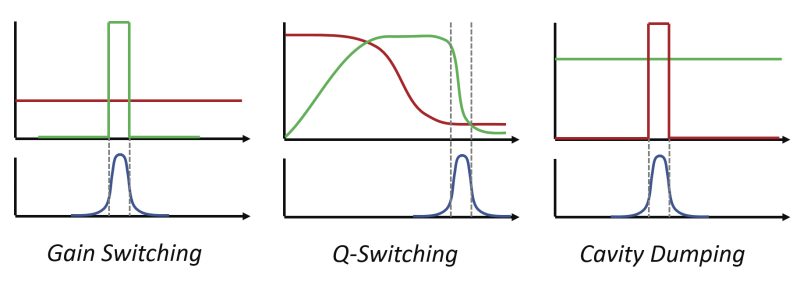
For steady-state lasing, the gain remains at a threshold value because the stimulated emission depletes the population inversion as rapidly as it is produced by the pumping rate. However, if the gain medium is pumped much faster than the steady-state value, a transient effect called gain switching can occur. In this case, the population inversion (and hence the gain coefficient) builds up much faster than the rate of stimulated emission within the laser cavity. The photons in the cavity experience an enormous amount of gain leading to a rapid increase in laser intensity. This, in turn, causes significant stimulated emission that rapidly depletes the population inversion. The result is a short pulse of light (see Figure 2). Gain switching is a modulation approach where the gain is controlled by turning the pumping source on and off. This can be accomplished by flashlamp pumping, which yields pulses in the µs to ms range. However, gain switching is most commonly applied to semiconductor lasers since it is straightforward to modulate the electric current that is used for pumping. This can lead to pulses ranging from a few ns to tens of ps and with repetition rates up to several GHz. This method is often utilized to generate laser sources for optical telecommunications where it is desirable to have high repetition rates to increase the amount of information transmitted per unit time.
Q-Switching
Q-switching also involves storing energy in the laser gain medium but not by modulating the pump source. Here, the laser pumping process is allowed to build up a population inversion far in excess of the typical threshold value by ensuring that the cavity losses are large, which prevents lasing. Inhibiting the optical feedback is accomplished by adding a loss in the laser cavity. After a large inversion has been achieved, the cavity feedback is switched back on. The laser then experiences gain that greatly exceeds losses, and the stored energy is released as a short and intense light pulse (see Figure 2). The quality factor (Q) is the ratio of the energy stored in a cavity to its energy loss per cycle. Since this modulation approach involves switching the cavity Q from a low value to a high one, it is designated Q-switching. Devices used for Q-switching must be able to rapidly modulate the cavity Q to generate short pulses and are grouped into two categories, active and passive. Active devices require an external operation to induce modulation which include acousto-optical switches, electro-optical shutters, and rotating mirrors. Passive devices switch automatically based on the non-linear optical response of the element being used, e.g., saturable absorption in organic dyes or semiconductors. Q-switching results in ns laser pulses with very large pulse energies of mJ or greater. They often operate with repetition rates between a few Hz and many kHz.
Cavity Dumping
In contrast to the techniques above which store energy in the laser medium via a population inversion, cavity dumping stores energy in the photons within the resonator. The losses within the resonator are kept low for some time by keeping the cavity mirror transmittances negligible, effectively trapping the photons in the cavity and allowing an intense pulse to build up. This pulse is extracted by switching an intra-cavity element after one round trip and “dumping” the pulse out of the cavity (see Figure 2). The optical switch typically is an acousto-optic modulator or electro-optic shutter. One benefit to cavity dumping over Q-switching is that the latter requires that the pulse duration increase when the pulse repetition rate increases. However, cavity dumping allows for very high pulse repetition rates, e.g., several MHz, while maintaining pulse durations of a few ns. Cavity dumping can be combined with other pulse generation techniques in order to allow for extraction of higher pulse energies than would typically be available using other techniques.
Mode-Locking
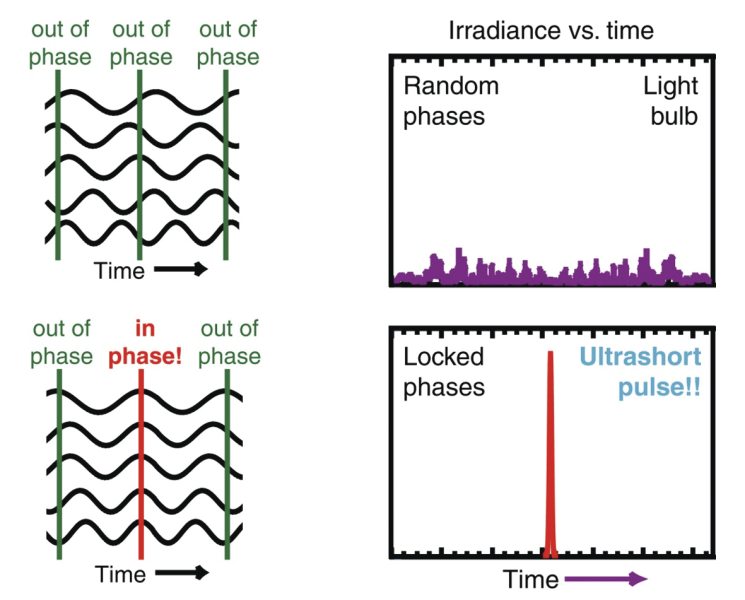
The pulse-generation techniques described above produce pulses that are limited to a few ns. To achieve ultrafast pulses with durations down to a few fs, a technique known as mode-locking is utilized where the cavity losses are modulated periodically at the round-trip time of the laser pulse. Unlike the other approaches which are based on transient effects within a laser cavity, mode-locking is a dynamic steady-state process. Many longitudinal modes can participate in the lasing process and yet they are not necessarily in phase with one another upon arrival at a cavity mirror leading to random fluctuations in the output power. However, if these laser modes can be coupled together such that they are all brought into phase at the mirror, constructive and destructive interference can occur, resulting in the generation of an ultrashort pulse (see Figure 3). The coupling of these modes is achieved using a very fast intracavity shutter which operates at the intervals of the round trip of the laser pulse and effectively coordinates the time of arrival of these modes, thereby locking their phases. Like Q-switching, mode-locking devices can be active or passive. Active devices that require external modulation include various amplitude and phase modulators. Passive devices rely on non-linear optical effects in suitable materials, including both slow and fast saturable absorption as well as intensity-dependent changes in the refractive index.
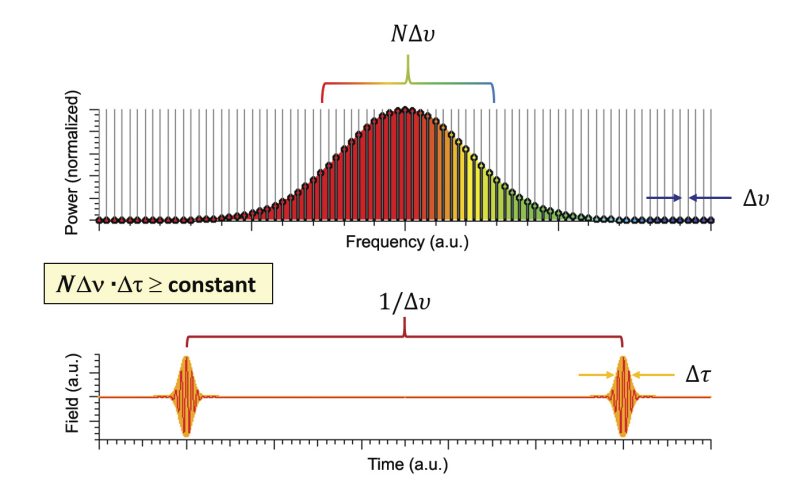
It is possible for all the longitudinal modes under the gain bandwidth to lase simultaneously, giving rise to a laser bandwidth of NΔν. If these modes are also locked together in phase, they interfere with each other to produce a series of intense pulses separated in time behaving like Fourier components of a periodic function. As shown in Figure 4, the separation of these pulses in time is simply the reciprocal of their frequency separation (i.e., 1/Δν) which is approximately 1-10 ns based on typical cavity lengths. Furthermore, based on a time-bandwidth Fourier relationship, the pulse duration (τ) is proportional to the inverse of the laser bandwidth. Since the laser bandwidth is largely dictated by the gain bandwidth of the medium, the narrowest pulses are produced from lasers with the largest gain bandwidth. Mode-locked solid-state lasers typically possess pulse durations ranging from 30 fs to 30 ps, operate at large repetition rates e.g., MHz to GHz, and generate moderate pulse energies e.g., pJ to tens of nJ. Achieving larger pulse energies (e.g., up to a few mJ) is possible, at the expense of the repetition rate, e.g., typically kHz, by incorporating cavity dumping or regenerative amplifiers
.