Light-Matter Interactions in Lasers
Light-Matter Interactions in Lasers
Light-Matter Interactions in Lasers
Light is generated from a laser as a result of the following process: electrons in a material move from an excited energy level to a lower-lying energy level and produce photons that contribute to the laser beam. Therefore, fundamental interactions between light and matter are the basis for the analysis of laser operation and the properties of laser light . This section provides an abridged description of the interactions between atoms/molecules in a laser material and the photons that make up the resulting laser light.
Energy Levels
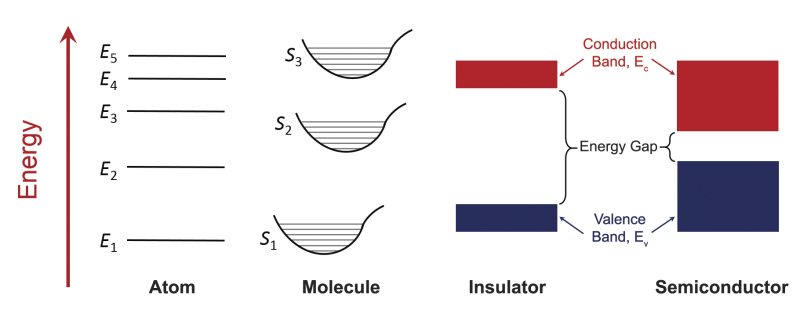
Atomic energy levels are determined by the interactions of the electrons with the atomic nucleus and other electrons. As electrons move or transition from one energy level to another, specific amounts of energy are either absorbed or emitted. This is the main mechanism by which photons of light can interact with atoms of matter. These energy levels and their associated photon energies are uniquely dependent on the electronic structure of the atom. Figure 1 shows a generic energy-level diagram for an atom. Molecules are made up of two or more atoms and their energy levels are dictated by the interatomic forces. In addition to electronic transitions, molecules also possess transitions associated with vibrational and rotational interactions which lead to a more complex set of energy levels compared to simple atoms (see Figure 1). For a large group of identical atoms/molecules where the constituents are isolated from one another, such as in a dilute gas, each atom/molecule has the same set of discrete energy levels. However, when atoms/molecules are brought close together, such as in liquids or solids, a variety of intermolecular interactions become increasingly important and the initially discrete energy levels associated with the isolated atoms or molecules gradually broaden into collections of numerous, densely spaced energy levels that form energy bands. These valence and conduction bands and their separating energy gaps are shown in Figure 1 for an insulator and a semiconductor.
Radiation Processes
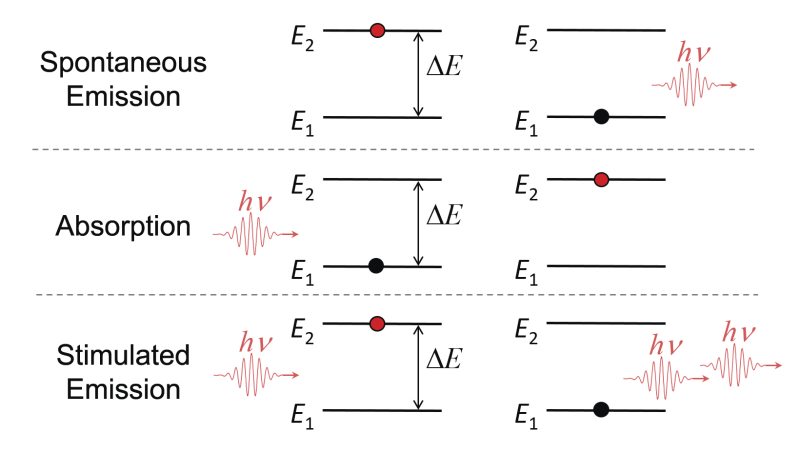
Regardless of the type of matter that makes up a material, there are three fundamental processes by which light interacts with atoms, creating upward and downward transitions between energy levels. Figure 2 shows the process known as spontaneous emission, which occurs when an atom is in an upper energy level (E2) or excited state and decays spontaneously to a lower energy level (E1), radiating a photon of light when it does so. Since each material has a unique set of energy levels, the emitted photons possess energies that are specific to that material. These photon energies are related to the frequency (ν) and wavelength (λ) of the light by:
ΔE = hν = hc / λ
where h is Planck's constant and c is the speed of light. The second process shown in Figure 2 is absorption. Absorption occurs when the atom is initially in the lower energy level and a photon with energy hν is absorbed by the atom raising it to the upper energy level. The final process in Figure 2 is stimulated emission. Emission is essentially the inverse process of absorption since it also requires a photon of energy hν to be present, but the atom is initially in the upper energy level. The photon stimulates the atom to radiate a duplicate photon having the same characteristics as the original, including energy, direction, phase and polarization. These properties are discussed further in Characteristics of Laser Output. Stimulated emission produces photons at the expense of energy stored in atoms which gives rise to amplification of the light or optical gain. This phenomenon is central to the operation of a laser and will be discussed in detail in Required Components for Lasing.
Transition Cross Section
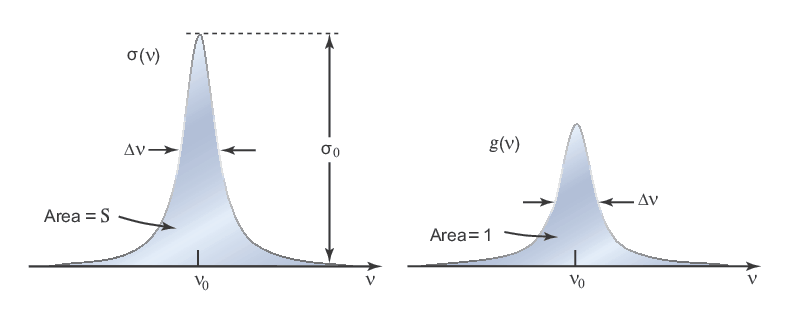
One term useful in quantitatively characterizing these atom-radiation interactions is the transition cross section σ(ν). This value describes the strength or probability that the interaction will occur and is applicable to all three of the radiation processes discussed above. As illustrated in Figure 3, the transition cross section is dependent on the frequency or wavelength of the photon of interest. It is centered on the resonance frequency (ν0), where σ(ν) is largest, and drops as ν deviates from ν0. A few key quantities of interest are the peak transition cross section, σ0 = σ(ν0), the linewidth (Δν) representing the full width at half maximum value (FWHM), and the area (S), which is called the transition strength or oscillator strength. A common way to write the transition cross section is in terms of its strength and profile:
σ(ν) = Sg(ν)
where the lineshape function g(ν) is a normalized function with unity area. This allows one to separate the strength of a transition from its frequency dependence. A number of processes contribute to the Δν associated with g(ν) including homogenous and inhomogenous broadening. Since the above equation applies to stimulated emission, its importance in the laser amplification/gain process should be clear. A large transition strength can give rise to a large gain coefficient for lasing, while the lineshape helps determine the frequency response and gain bandwidth (see Characteristics of Laser Output for more information)..
Population Inversion
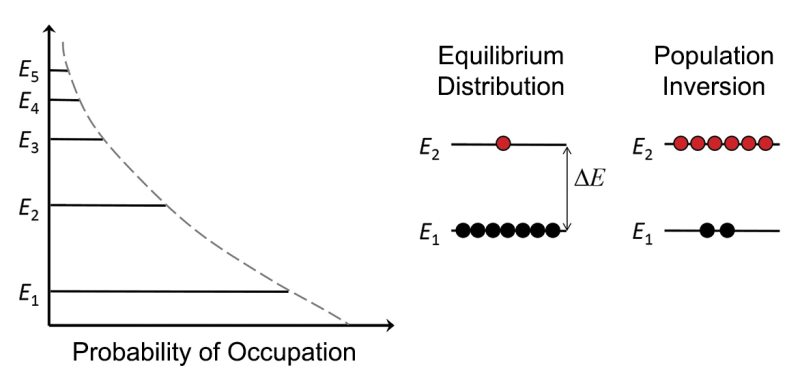
The depictions of the radiation processes (Figure 2) illustrate that their impact is tied to the population of the atoms in the various energy levels. For a system in thermal equilibrium, the probability that an atom is in a particular energy level is given by the Boltzmann distribution. As shown in Figure 4, this probability exponentially decreases with increasing energy level. If one considers just two energy levels, E2 and E1 (see Figure 4), then the Boltzmann distribution gives the ratio of their respective populations, N2 and N1, as
N1 / N2 = exp ( - ΔE / kT)
where k is the Boltzmann constant and T is the temperature. Typical energy level differences (ΔE) for laser transitions are two orders-of-magnitude larger than kT at room temperature and so N2/N1 << 1. Since most of the population is in the lowest energy level, the process of absorption dominates, which is typically how light interacts with most matter. Furthermore, with little population in the upper energy level, stimulated emission is highly unlikely. However, if significant population could be transferred to the higher level such that N2 exceeds N1, a non-equilibrium condition known as a population inversion can be achieved. Population inversion is a prerequisite for laser action, since stimulated emission is the means by which amplification is achieved.