Pulse Compression With Diffraction Gratings
Pulse Compression With Diffraction Gratings
Pulse Compression and Stretching with Diffraction Gratings
Pulse compression is a useful technique that takes advantage of the relationship between pulse duration and spectral width of a pulse. This enables the amplification of laser pulses above the normal damage threshold limits imposed by the optical components in the laser system. Diffraction gratings, used in conjunction with chirped pulses, are the key to compressing or stretching a laser pulse (i.e., increasing or decreasing their peak power with little loss in energy).
Pulse Compression
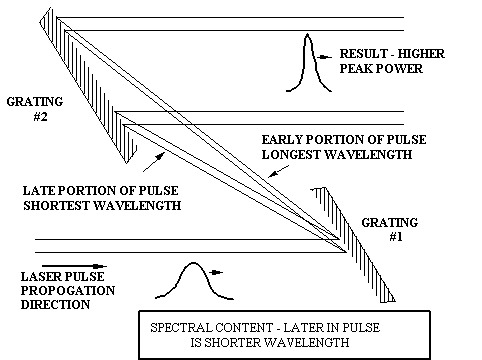
When a spectrally broad laser pulse is incident on a diffraction grating, the various wavelengths that make up the pulse will diffract from the grating at angles that depend on wavelength. If this pulse has its wavelength "chirped" so that the frequency increases during the length of the pulse, then diffraction will spread out the light in proportion, with the first part of the pulse (longer wavelengths) diffracting at a larger angle. The trailing portion of the pulse (shorter wavelengths) will diffract at a smaller angle and is directed to the leading edge of the second grating (see Figure 1). When the light diffracts from the second grating, which is oriented parallel to the first grating, the different parts of the pulse (with their correspondingly different wavelengths) will diffract at angles which yield a pulse whose parts are nearly in time synchronism. Peak power greatly increases, while total energy remains nearly the same.
Pulse Stretching
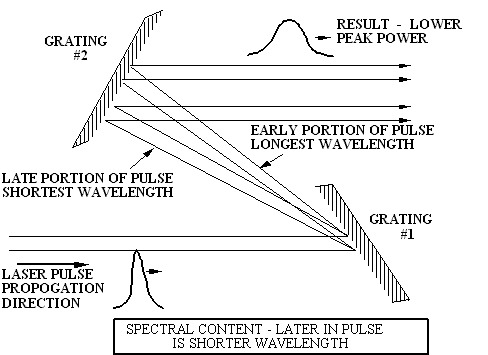
A pulse is sometimes stretched instead, in order to extract the maximum stored energy as well as reduce possible damage to optical components from excessive powers. This can be accomplished by using a pair of gratings in an "antiparallel" arrangement (see Figure 2). This works exactly opposite to the compression scheme in that the chirped pulse is spread out more by the gratings so that the resulting laser beam is longer in duration.
Dispersion
The grating equation mλ=d(sinα + sinβ) can be differentiated to give the angular spread (dispersion) of the spectrum:
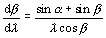
Here α and β are the angles of incidence and diffraction, m is the diffraction order, λ is the wavelength and d is the groove spacing.
Master Grating Options for Pulse Compression
Gratings used for pulse compression of lasers generally require a diffracted wavefront free of aberrations as well as high diffraction efficiency. Several of our gratings, both ruled and holographic, can be used for pulse compression at wavelengths of 800 nm, 1.06 μm, 1.3 μm, 1.5 μm, etc. The groove frequencies most commonly used are 300 g/mm, 600 g/mm, 1200 g/mm and 1800 g/mm. Nominal Blaze wavelengths listed are for the first-order Littrow configuration. The maximum ruled area is groove length x ruled width. Click on a Master Grating Code (last 4 digits of a grating's part number) below to view master grating efficiency curves. Use the request a quote to get a quote based on your requirements. We are continually developing new gratings, so please contact us if you have a question regarding the best grating for your particular application.
| Master Grating Code | Grooves per mm | Nominal Blaze Wavelength | Nominal Blaze Angle (R) or Modulation Depth (H) | Maximum Ruled Area (mm) | Request a Quote |
|---|---|---|---|---|---|
| 430H | 2400 | 300 nm | high | 102 x 102 | Quote |
| 059H | 2000 | 750 nm | high | 102 x 128 | Quote |
| 330H | 1800 | 500 nm | high | 102 x 128 | Quote |
| 233H | 1760 | 550 nm | high | 102 x 102 | Quote |
| 239H | 1500 | 750 nm | high | 102 x 102 | Quote |
| 230H | 200 | 800 nm | high | 110 x 110 | Quote |
| 340R | 1200 | 600 nm | 21.1° | 204 x 306 | Quote |
| 360R | 1200 | 750 nm | 26.7° | 156 x 206 | Quote |
| 727R | 672 | 832 nm | 16.4° | 64 x 64 | Quote |
| 351R | 600 | 800 nm | 13.9° | 154 x 206 | Quote |